|
||||||
|
||||||
Determinare il massimo valore del carico T di taglio che si può applicare ad una sezione come quella rappresentata in figura (dimensioni in mm) supponendo che il valore della samm sia pari a 120 N/mm2.
Il valore massimo della tensione tangenziali di taglio si ha in corrispondenza dell'asse neutro. Poiché la sezione non presenta simmetria occorre calcolare la posizione del baricentro suddividendo la figura in aree elementari per successivamente applicare il teorema di Varignon.
Scelta una opportuna suddivisione delle figure e un sistema di riferimento si costruisce la tabella per il calcolo del baricentro:
Individuata la posizione del baricentro si assume che la tensione tangenziale massima in corrispondenza del baricentro stesso sia pari al valore della tensione tangenziale ammissibile tamm.
Tale valore si ricava
dalla conoscenza del valore della tensione normale ammissibile samm
= 120 [N/mm2]: 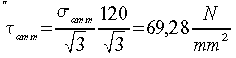 .
.
Per determinare il valore
del taglio T basterà ricavare il valore dalla formula per il calcolo
della tensione di taglio:
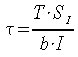
nella quale si sostituirà opportunamente a t il valore tamm.
Per il calcolo della forza
di taglio si utilizzerà allora l'espressione:
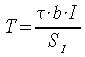
determinando preventivamente il valore del momento statico della parte di
sezione sovrastante l'asse neutro.
Per ottenere questo risultato occorre sommare i prodotti delle aree elementari per la distanza dei rispettivi baricentri dall'asse neutro (stesso procedimento utilizzato per il calcolo del baricentro). Prendendo in considerazione la figura ottenuta considerando la parte di sezione sovrastante l'asse neutro si ottiene:
Creando una tabella per il calcolo del momento statico: 
da cui otteniamo:
Per il calcolo del momento di inerzia di tutta la sezione si completa la tabella utilizzata per il calcolo dell'asse neutro
Così, sostituendo i valori delle grandezze, otteniamo:
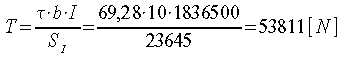
che è il valore della sollecitazione di taglio T tale da generare una
tensione tangenziale sull'asse neutro pari al valore della ![]() .
.
Per determinare l'andamento delle tensioni tangenziali nei punti di maggior interesse della sezione occorre procedere al calcolo dei valori dei vari momenti statici.
I momenti statici relativi
a A e G sono nulli per cui le tensioni tangenziali all'altezza di A e G sono
nulle; per il calcolo negli altri punti notiamo che il momento statico è
lo stesso in B e C ed anche in E e F. Ricordando che il valore del momento
statico si può ricavare dal prodotto dell'area della figura interessata
e cioè ![]() avremo:
avremo:
- per la figura 1
- per la figura 3
da cui ricaviamo:
L'andamento delle tensioni tangenziali risulta quindi: