MECCANICA

voti
papers
programmi

galileo
links

test

 

OMAR
FAUSER

Registro OnLine:
Omar
Fauser
Ossola

Innanzitutto chiediamoci perché dobbiamo avventurarci in una impresa così impervia quale la progettazione di una coppia di ruote dentate. I motivi sono molteplici, probabilmente vorrete prendere un bel voto nel prossimo compito in classe, forse avete anche la speranza di riuscire a fare una discreta prova scritta all'esame di maturità... quale che sia il nobile motivo che vi spingerà nella vita a questa dura scelta queste poche righe cercheranno di darvi un minimo aiuto.

Come iniziare? Quale che sia il modo in cui la frittella vi viene presentata lo scopo ultimo di una coppia di ruote dentate è sempre quello di trasmettere una potenza, o se volete una coppia. Non sapete cosa significa trasmettere una potenza o una coppia? Bene... anzi male, andate fino al parco della vittoria senza passare dal via.

Una potenza viene fornita generalmente da un motore, sia esso elettrico a combustione interna, idraulico, etc... Generalmente il nostro motore avrà una determinata velocità di rotazione e a questo motore, in qualche modo che a noi per il momento non interessa, è collegato un albero che ruota. Da qualche parte su quest'albero si trova una delle due ruote dentate della nostra coppia di ruote, l'altra si trova molto, ma molto vicino, su un altro albero che ruota o un pò più lento o un pò più veloce... da questa ambiguità nascono i cosiddetti riduttori e moltiplicatori. Nei riduttori la ruota che è collegata all'albero motore ha un numero di denti inferiore di quella montata sull'albero condotto, il quale ruoterà più lentamente di quello motore, viceversa nel caso dei moltiplicatori.

Poiché esiste una chiara relazione matematica tra la Potenza P, il momento motore M e la velocità di rotazione w data da è ovvio che (poiché si suppone che il motore eroghi una potenza costante, mentre sappiamo che la velocità di rotazione dei due alberi è diversa) risultadiverso il momento torcente tra albero motore ad albero condotto.
Questa relazione assume significato nel momento in cui si assegnano alle grandezze in questione le unità di misura appropriate. E' infatti è possibile che le grandezze in questione vengano misurate con unità che possono essere le più disparate per cui è necessario prestare un minimo di attenzione quando si vanno a sostituire i valori numerici nelle espressioni letterali. La cosa migliore da fare sarebbe usare le unità del S.I., ovvero potenza in [Watt], momento torcente in _[Nm] e la velocità angolare in _[rad/sec] . Qualora, come spesso accade, le grandezze in oggetto vengano fornite con unità di misura differenti sarebbe opportuno convertirle in unita del S.I.

Es: se la velocità di rotazione è espressa in giri al minuto, solitamente indicati con la lettera n, è possibile trasformarla nella unità S.I. tramite la relazione:. Occorre prestare attenzione all'unità di misura della potenza, molto spesso infatti si utilizzano i kW, che ovviamente corrispondono a 1000 watt.

Fatta questa doverosa premessa siamo in linea di massima in grado di calcolare il momento sull'albero motore e il momento sull'albero condotto una volta note la potenza da trasmettere e le velocità dei due alberi. E` però opportuno precisare che la potenza che deve essere utilizzata nel dimensionamento non è in generale la cosiddetta potenza di targa del motore, ma la potenza di calcolo che tiene conto del tipo di utilizzo che si intende fare della nostra coppia di ruote dentate. Per ottenere la potenza di calcolo occorre moltiplicare la potenza di targa per un coefficiente noto come fattore di servizio f_{s, valore} reperibile sulle tabelle nei manuali specializzati e non, che dipende dal tipo di servizio a cui è sottoposta la coppia di ruote, dal tipo di utilizzatore, etc.

Per gli amanti delle tabelle viene di seguito riportata una tabella con alcuni valori del coefficiente di servizio

Tipo di servizio	durata del pieno carico normale
	Breve				Lunga
	Servizio Intermittente	Servizio Normale	Servizio continuo	Servizio Intermittente	Servizio Normale	Servizio continuo
senza sovraccarico o con sovraccarico breve e saltuario	0,5÷,7	0,8÷,9	1	0,7÷0,8	1÷1,1	1,2÷1,5
con sovraccarico del 25-100-200% breve e frequente	-	-	-	0,8÷1,5	1,1÷2	1,6÷2,5
con sovraccarico del 25-100-200% non breve o assai frequente	-	-	-	0,9÷2	1,2÷3	1,8÷4

Come si può vedere la potenza di targa può aumentare sino a 4 volte se il funzionamento presenta sovraccarichi frequenti ed elevati ed il servizio è continuo (ca. 20÷24 ore giornaliere).

Le ruote dentate, come è noto, vengono proporzionate in base a un modulo unificato: due ruote aventi lo stesso modulo possono (in linea di massima) ingranare tra di loro, mentre due ruote aventi moduli diversi non possono. Il calcolo del modulo può essere effettuato seguendo due percorsi diversi ma al tempo stesso legati tra di loro. Chiameremo calcolo a resistenza il primo e calcolo ad usura il secondo. Entrambi i metodi di calcolo devono essere usati, l'ordine da seguire dipende dal tipo di materiale scelto, se si tratta di un materiale di cui sono garantite le caratteristiche di resistenza si effettuerà un proporzionamento a usura e una successiva verifica a resistenza, nel caso di materiali induriti superficialmente si può supporre che la durezza superficiale del dente garantisca la resistenza del dente, per cui il proporzionamento si farà utilizzando il calcolo a resistenza per poi verificare a usura.

Le due tabelle seguenti elencano le caratteristiche dei materiali da usare per la costruzione delle ruote dentate, la prima relativa ai materiali da progettare a usura, la seconda per i materiali da progettare a resistenza.

Materiali per ruote dentate, dimensionamento a usura:

Materiale	sr	HB	Pam	sam
Ghise grigie
UNI G25	245	220	460	50
Ghise sferoidali
UNI G20	195	205	410	40
UNI GS 55/2	540	190÷250	440÷530	110
ASTM 60	740÷880	270÷350	560÷660	145
Acciai in getti
UNI Fe 52	510	145	330	100
Acciai da fucinare
UNI Fe 50	490÷590	150	390	130
UNI Fe 60	590÷680	175	430	145
Acciai da bonifica
UNI C40	700÷840	220	490	155
UNI C50	760÷900	245	530	175
UNI 38 NiCrMo 4	980÷1130	300	650	225
UNI 40 NiCrMo 7	1030÷1180	330	710	235

Materiali da progettare a resistenza:

Materiale	sr	HV	Pam	sam
Acciai da tempra a induzione
UNI C48	760÷900	670÷760	1250÷1350	175÷215
UNI 40 Ni Cr Mo 4	980÷1130	630÷720	1200÷1300	215÷265
Acciai da cementazione
UNI 16 Cr Ni 4	1080÷1420	670÷760	1200÷1300	215÷265
UNI 20 Cr Ni 4	1230÷1570	720÷810	1300÷1400	245÷295
UNI 18 Ni Cr Mo 5	1230÷1520	720÷810	1300÷1400	245÷295
Acciai da nitrurazione
UNI 42 Cr Al Mo 7	930÷1080	850	1200÷1300	215÷265
UNI 38 Cr Al Mo 7	930÷1080	1000	1200÷1300	215÷265

_{La formula consigliata dal manuale di meccanica per il progetto a usura è}

dove le grandezze che compaiono nella formula hanno il seguente significato:

M₁ : Momento sull'albero motore [N*mm]

C : coefficiente tabellato che dipende dal numero di denti del pignone e dal rapporto di trasmissione

f_v : fattore di velocità, tiene conto dell'aumento della sollecitazione dovuto alla velocità periferica

p_amm : pressione ammissibile del materiale ricavata da tabella

l : rapporto tra larghezza della ruota dentata e modulo, questo valore dipende dal tipo di costruzione e assume dei valori che possono essere ricavati da una apposita tabella

Di seguito si riportano le tabelle da usare con la formula in questione.

Rapporto di ingranaggio z2/z1
Z1	Ingranaggio esterno				Pignone / dentiera	Ingranaggio interno
	1	1.33	2	4		4	2
14	17.3	16.9	16.4	15.8	15.1	------	-----
16	15.6	15.2	14.7	14.1	13.4	-----	----
18	14.3	14.0	13.4	12.9	12.1	11.3	----
20	13.3	12.9	12.4	11.8	11.2	10.3	9.2
22	12.4	12.0	11.6	11.0	10.3	9.6	8.5
25	11.3	11.0	10.6	10.0	9.4	8.6	7.6
28	10.6	10.2	9.7	9.3	8.7	7.9	7.0
32	9.6	9.3	8.9	8.4	7.8	7.2	6.4
36	8.9	8.6	8.2	7.7	7.2	6.6	5.8
40	8.3	8.0	7.6	7.2	6.7	6.1	5.4
50	7.1	6.8	6.5	6.2	5.8	5.3	4.6
60	6.3	6.1	5.8	5.5	5.1	4.7	4.1

I valori del coefficiente C dipendono quindi dal numero di denti del pignone e dal rapporto di trasmissione, ovviamente capiterà sempre di dover scegliere un coefficiente per un numero di denti e per un rapporto di trasmissione non presenti in tabella, in questo caso non infrequente si può senza problema interpolare linearmente tra i due valori più vicini. Pare che interpolare linearmente non sia lo sport preferito dagli studenti, ma con un esempio forse sarà possibile ridurre la difficoltà dell'operazione.

Supponiamo di avere come numero di denti z₁ = 27 e rapporto di trasmissione i = 3, i valori da scegliere dalla tabella dovranno essere compresi tra:

x₁ = 25 , y₁ = 10.6
x₂ = 28, y₂ = 9,7

per la prima interpolazione al valore x_d = 27 e rapporto di trasmissione i= 2.

Per la seconda interpolazione scegliamo tra: sempre per x_d = 27 ma con rapporto di trasmissione i = 4

x₁ = 25 , y₁ = 10.6
x₂ = 28, y₂ = 9.3

Graficamente è possibile rappresentare i due punti in un piano cartesiano tracciando successivamente il segmento che li congiunge dall'analisi del grafico è possibile ricavare la seguente espressione: (vedere sul testo di matematica la voce equazione di una retta che passa per due punti, oppure scrivere la relazione di proporzionalità tra i due triangoli che si possono individuare nella figura)

sostituendo i valori numerici otteniamo :

per la prima interpolazione y_d = 9,73 con x_d 27 per i = 2

per la seconda interpolazione y_d = 9.53 x_d = 27 per i = 4

A questo punto la parte di tabella che ci interessa ha una nuova riga

	2	3	4
25	10,6		10,0
27	10,00		9,53
28	9,7		9,3

ora con la stessa formula interpoliamo trai i punti di coordinate

x₁ = 2 , y₁ = 10.0

x₂ = 4, y₂ = 9.53

e otteniamo i valori desiderati y_d = 9.765 x_d = 3 per z₁ = 27

in questo modo si completa la tabella col valore cercato:

	2	3	4
25	0,4		0,4
27	10,0	9,765	0,4
28	0,4		0,4

La scelta del numero di denti da assegnare al pignone, necessaria per poter calcolare il coefficiente C deve essere preceduta da alcune brevi considerazioni:

a) scegliere un numero di denti Z₁ superiore a quello minimo ricavabile dalle apposite tabelle

b) il numero di denti Z₁ fermo restando l'assunto del punto a) dovrà essere tanto più basso quanto più esistono problemi di ingombro

c) se non esistono problemi di ingombro è opportuno scegliere un numero Z₁ tanto più grande quanto maggiore sarà la velocità di rotazione

d) quando possibile scegliere un numero di denti per la ruota che non sia un esatto multiplo della condotta (per evitare deformazioni dovute al fatto che sono sempre gli stessi denti a ingranare tra loro), l'ideale sarebbe che Z₁ e Z₂ fossero primi tra loro

Dalla seguente tabella è possibile ricavare il numero minimo pratico di denti per il pignone:

Numero minimo di denti per il pignone

Rapporto di ingranaggio	Angolo di pressione a=20°	Angolo di pressione a=15°
5	14	23
2.5	13	21
1.67	12	20
1.25	11	19
1	11	18

Una breve considerazione sul coefficiente l, che come detto rappresenta il rapporto b/m tra larghezza ruota e modulo della stessa, questo viene scelto in fase di progetto secondo i criteri che sono esposti nella tabella seguente, tenendo conto che l può essere tanto più grande quanto maggiore sarà la rigidità dei supporti e dei cuscinetti.

Larghezza degli ingranaggi

Tipo di costruzione	l=b/m
supporti su telai di ordinaria carpenteria, montaggi a sbalzo o comunque poco rigidi	10÷15
supporti in scatola e casi analoghi	20÷25
cuscinetti di esecuzione molto accurata, supporti e alberi rigidi	25÷30

Premesse queste brevi (si fa per dire) note occorre prendere in considerazione il fattore di velocità, si tratta di un coefficiente che tiene conto degli effetti dinamici di sovraccarico, che traggono origine dalle imperfezioni geometriche della dentatura e che si accentuano con la velocità periferica elevata. Anche questo coefficiente (tanto per cambiare) si trova tabellato in funzione della velocità periferica, della precisione della ruota e dello stato di indurimento superficiale.

Fattore di velocità f_v

	dentature precise o correnti rodate		dentature correnti
velocità periferica	non indurite	indurite
0.5	0.75	0.92	0.54
1	0.63	0.87	0.46
2	0.59	0.82	0.43
5	0.55	0.75	0.40
10	0.50	0.65	------

valori simili (non uguali) possono ottenersi tramite formule empiriche reperibili sui manuali tecnici del tipo: f_v = 0.85 - 0.013v, per ruote precise non indurite, oppure f_v = 0.65 - 0.002v per dentature correnti

E` evidente che non è possibile conoscere la velocità periferica, e quindi il fattore f_v se prima non si conosce il diametro della ruota, cosa impossibile prima di averne calcolato il modulo, per questo motivo il calcolo della ruota deve avvenire per tentativi, supponendo un opportuno valore iniziale del coefficiente f_v che dovrà poi essere verificato con un calcolo iterativo (quelli che non conoscono il significato della parola iterativo possono a questo punto prendersi un piccolo break e fare una passeggiata fino alla biblioteca comunale dove potranno con comodo consultare i migliori dizionari della lingua italiana).

Dal primo calcolo si ottiene quindi un valore m del modulo, che dovrà essere arrotondato al valore unificato più vicino. Con questo primo valore si calcola il diametro primitivo:

nota la velocità angolare w [rad/s] è possibile risalire alla velocità periferica

naturalmente si otterrà il risultato in metri al secondo solo se si avrà la accortezza di trasformare il valore del raggio da millimetri a metri.

Noto questo primo valore di v si può ora calcolare il fattore di velocità f_v e ricalcolare il modulo. Se il valore (unificato) ottenuto coincide con quello precedente si può procedere al calcolo di verifica, in caso contrario si procede a un altro tentativo ricalcolando m. d_p, v.

Il calcolo di verifica deve essere effettuato valutando l'altra sollecitazione (quella non considerata nel primo calcolo) per cui, nello specifico, utilizzando la formula per il calcolo a resistenza:

In questo caso, trattandosi di una verifica, non è più necessario calcolare il fattore f_v per tentativi, il valore ottenuto durante il calcolo di progetto sarà già il valore da usare. Il coefficiente G è tabellato in funzione del numero di denti del pignone:

Coefficiente G per ruote normali

z	G	z	G	z	G	z	G
14	0,71	25	0,54	50	0,40	-400	0,19
16	0,67	38	0,51	70	0,36	-200	0,24
18	0,63	32	0,48	100	0,32	-100	0,30
20	0,60	36	0,46	200	0,25	-70	0,34
22	0,57	40	0,44	400	0,23	-50	0,37

Per i materiali della tabella relativa ai materiali da indurimento superficiale si segue un procedimento analogo, ma il modulo di progetto viene calcolato utilizzando la formula col coefficiente G (ferme restando tutte le considerazioni precedenti) per poi eseguire la verifica utilizzando la formula con C.

E' importante notare che il modulo su cui si basa il proporzionamento delle ruote dentate è una grandezza unificata, i cui valori si possono ricavare dalla tabella seguente:

Tabella dei moduli unificati:

Preferire	1	1,25	1,50	2	2,50	3	4	5	6	8	10	12	16	20
Ammessi	1,125	1,375	1,75	2,25		3,50		4,50	5,50	7	9	11	14	18
Evitare						3,25	3,75		6,50

 

Ruote a denti elicoidali
In queste ruote il dente ha un imbocco prolungato, così che è maggiore il numero delle coppie di denti simultaneamente in presa. Sono pertanto adatte a ingranaggi veloci e silenziosi. Si chiama angolo d'elica b l'angolo formato dall'asse del dente con la generatrice del cilindro primitivo. Si assume b = 15°÷ 30° per dentature di piccola larghezza; Per dentature più larghe b = 5°÷15°. (Si sceglieranno angoli inferiori (10°) per ruote lente e maggiori (45°) per ruote velocissime.

Si distingue il modulo trasversale m_t = d/z dal modulo normale m_t = m_n cos b . L'altezza del dente è proporzionata in base a m_n

L'interasse è:

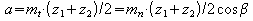
II numero ideale di denti è:

Il numero di denti minimo scende a 16, 14, Il con b = 10° 20°, 30° rispettivamente a_n = 20°)

Detta la componente periferica utile della spinta sui denti, la componente assiale è .

Il modulo si ricava con la formula delle ruote a denti diritti, salvo che al posto di C si pone il coefficiente C_el = 0,88 C (per b = 15°) C_el, = 0,83 C (per b = 30°) per ruote di ottima precisione.

Se le ruote hanno denti induriti, si calcola il numero di denti ideale ; si legge il corrispondente valore di G e lo si sostituisce.
Per le ruote di ottima precisione   con G_el = 0,93 G per b = 15°: G_el = 1,04 G per b = 30°
I valori di C_el, e di G_el vanno moltiplicati per 1,05÷ 1,10 se le ruote sono di costruzione meno precisa.

Le ruote bielicoidali, dei moderni riduttori, hanno la corona divisa in due metà con denti di opposte inclinazioni. É così compensata la spinta assiale. L'intera fascia dentata ha una larghezza b = 4 0 m_n ÷ 80 m_n per riduttori di piccola e media potenza; 80 m_n ÷ 200 m_n. per elevate potenze e accuratissima esecuzione.