|
||||||
|
||||||
Si deve progettare una trave a sezione circolare cava, con rapporto d/D=0.8, adatta a resistere ad un carico di punta P=50kN. La trave risulta incastrata ad una estremità, incernierata all'altra e lunga 3 metri. Utilizzare il metodo omega ed eventualmente verificare i risultati con un altro metodo conosciuto.
Come primo tentativo conviene applicare la formula di Eulero, essendo la trave vincolata con incastro e cerniera si può ritenere che la lunghezza libera di inflessione sia data da:
e quindi ricavare il momento di inerzia con la formula di Eulero in cui si assume un grado di sicurezza a =5
Con la formula inversa si può ora ricavare il primo valore del diametro esterno:
Determinato il valore della tensione ammissibile:
si può procedere, con il metodo Omega, a ricavare il coefficiente dalla tabella relativa all'acciaio Fe 430 curva "a" :
Si procede calcolando il valor medio degli ultimi due valori del coefficiente di snellezza:
Il coefficiente di snellezza appena calcolato non si discosta di molto da quello precedente, si può quindi ritenere concluso il processo di iterazione, a questo punto si sceglie un valore unificato per il nostro diametro esterno e si procede alla verifica finale:
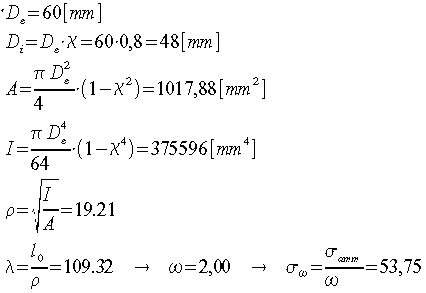
La tensione effettiva agente sulla trave risulta essere
inferiore alla tensione ammissibile calcolata col metodo Omega.
Il procedimento non cambia se si utilizza un materiale diverso, ad esempio un Fe 360.
Determinato il valore della tensione ammissibile:
Si può procedere ricavando il coefficiente dalla tabella relativa all'acciaio Fe 430 curva "a":
Si procede calcolando il valor medio degli ultimi due valori del coefficiente di snellezza:
Il coefficiente di snellezza oscilla ora tra i valori 113 e 107, si può quindi ritenere concluso il processo di iterazione, a questo punto si sceglie un valore unificato per il nostro diametro esterno e si procede alla verifica finale:
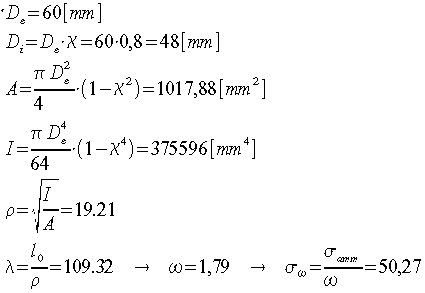
La tensione effettiva agente sulla trave risulta essere pari a:
Valore inferiore alla tensione ammissibile calcolata col metodo Omega.
Come si può facilmente notare il diametro finale calcolato col metodo Omega risulta lo stesso anche utilizzando un materiale con carico di rottura inferiore a conferma della tesi che nella sollecitazione di carico di punta non importa tanto la resistenza meccanica in sè, quanto l'elasticità del materiale; valore che per gli acciai dipende dal modulo di Young, che rimane invariato passando dal Fe 430 al Fe 360.