|
||||||
|
||||||
Discorsi e dimostrazioni matematiche
Il Saggiatore
La Bilancetta
Le Mecaniche
Le Lettere
Sidereus Nuncius
Trattato fortificazione
Papers
meccanica
sistemi
robotica
Galileo Galilei
LE MECANICHE
DIFFINIZIONI
Quello che in tutte le scienze demostrative è necessario di osservarsi, doviamo noi ancora in questo trattato seguitare: che è di proporre le diffinizioni dei termini proprii di questa facultà, e le prime supposizioni, delle quali, come da fecondissimi semi, pullulano e scaturiscono consequentemente le cause e le vere demonstrazioni delle proprietà di tutti gl'instrumenti mecanici. I quali servono per lo più intorno ai moti delle cose gravi; però determineremo primamente quello che sia gravità.
Adimandiamo adunque gravità quella propensione di muoversi naturalmente al basso, la quale, nei corpi solidi, si ritrova cagionata dalla maggiore o minore copia di materia, dalla quale vengono constituiti.
Momento è la propensione di andare al basso, cagionata non tanto dalla gravità del mobile, quanto dalla disposizione che abbino tra di loro diversi corpi gravi; mediante il qual momento si vedrà molte volte un corpo men grave contrapesare un altro di maggior gravità: come nella stadera si vede un picciolo contrapeso alzare un altro peso grandissimo, non per eccesso di gravità, ma sì bene per la lontananza dal punto donde viene sostenuta la stadera; la quale, congiunta con la gravità del minor peso, gli accresce momento ed impeto di andare al basso, col quale può eccedere il momento dell'altro maggior grave. È dunque il momento quell'impeto di andare al basso, composto di gravità, posizione e di altro, dal che possa essere tal propensione cagionata.
Centro della gravità si diffinisce essere in ogni corpo grave quel punto, intorno al quale consistono parti di eguali momenti: sì che, imaginandoci tale grave essere dal detto punto sospeso e sostenuto, le parti destre equilibreranno le sinistre, le anteriori le posteriori, e quelle di sopra quelle di sotto; sì che il detto grave, così sostenuto, non inclinerà da parte alcuna, ma, collocato in qual si voglia sito e disposizione, purché sospeso dal detto centro, rimarrà saldo. E questo è quel punto, il quale anderebbe ad unirsi col centro universale delle cose gravi, ciò è con quello della terra, quando in qualche mezzo libero potesse descendervi.
Dal che caveremo noi questa supposizione: Qualunque grave muoversi al basso così, che il centro della sua gravità non esca mai fuori di quella linea retta, che da esso centro, posto nel primo termine del moto, si produce insino al centro universale delle cose gravi. Il che è molto ragionevolmente supposto: perché, dovendo esso solo centro andarsi ad unire col centro comune, è necessario, non essendo impedito, che vadia a trovarlo per la brevissima linea, che è la sola retta. E di più possiamo, secondariamente, supporre: Ciascheduno corpo grave gravitare massimamente sopra il centro della sua gravità, ed in esso, come in proprio seggio, raccòrsi ogni impeto, ogni gravezza, ed in somma ogni momento. Suppongasi finalmente: Il centro della gravità di due corpi egualmente gravi essere nel mezzo di quella linea retta, la quale li detti due centri congiunge; o veramente, due pesi eguali sospesi in distanze eguali avere il punto dell'equilibrio nel commune congiungimento di esse uguali distanze: come, per essempio,
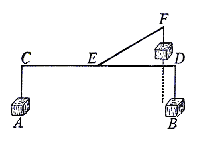
sendo la distanza CE eguale alla distanza ED, e da esse sospesi due pesi eguali, A, B, supponghiamo il punto dell'equilibrio essere nel punto E, non essendo maggior ragione di inclinare da una che dall'altra parte. Ma qui è d'avvertire, come tali distanze si devono misurare con linee perpendicolari, le quali dal punto della suspensione caschino sopra le linee rette, che dai centri della gravità delli due pesi si tirano al centro commune delle cose gravi. E però, se la distanza ED fusse trasportata in EF, il peso B non contrapeserebbe il peso A; perché tirandosi dai centri della gravità due linee rette al centro della terra, vedremo quella che viene dal centro del peso I esser più vicina al punto E, dell'altra prodotta dal centro del peso A. Devesi dunque intendere, i pesi eguali esser sospesi da distanze eguali, ogni volta che le linee rette, che dai loro centri vanno a trovare il centro commune delle cose gravi, saranno egualmente lontane da quella linea retta, che dal termine di esse distanze, ciò è dal punto della suspensione, si produce al medesimo centro della terra.
Determinate e supposte queste cose, verremo all'esplicazione di un comunissimo e principalissimo principio di buona parte delli strumenti mecanici, dimostrando come pesi diseguali pendenti da distanze diseguali peseranno egualmente, ogni volta che dette distanze abbino contraria proporzione di quella che hanno i pesi. Che pesi diseguali pesino egualmente, sospesi da distanze diseguali, le quali abbino contraria proporzione di quella che essi pesi si ritrovano avere, non solamente dimostreremo esser vero in quel modo che siamo certi della verità del principio posto sopra, dove si suppose pesi eguali pesare egualmente da distanze eguali; ma dimostreremo essere la medesima cosa per l'appunto, e che altro non è sospendere pesi diseguali da distanze di contraria proporzione, che pesi eguali da distanze eguali.
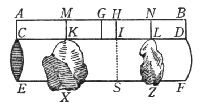
Intendasi dunque il solido grave CDFE, di gravità omogenea in tutte le sue parti, ed egualmente grosso per tutto, qual saria una figura colonnare o altra simile, il quale dalli estremi punti C, D sia sospeso dalla linea AB, eguale all'altezza del solido. Or dividendo essa linea AB egualmente nel punto G, e da esso sospendendola, non è dubbio alcuno che in esso punto G si farà l'equilibrio: perché la linea che da esso punto si tirasse rettamente al centro della terra, passerebbe per il centro della gravità del solido CF, e di esso intorno a detta linea consisterebbono parti di eguali momenti, e saria il medesimo che se dai punti A, B pendessero due metà del grave CF. Intendasi adesso, esser detto grave secondo la linea IS tagliato in due parti diseguali; è manifesto che la parte CS, come ancora l'altra SD, non staranno più in tale sito, non avendo altri sostegni che li due legami AC, BD. Però, venendo al punto I, intendasi aggiunto un nuovo legame, il quale fermato al punto H, perpendicolarmente sopraposto al taglio IS, sostenga comunemente nel pristino stato l'una e l'altra parte del solido: dal che ne séguita che non si essendo fatta mutazione alcuna, o di gravità o di sito, nelle parti del solido rispetto alla linea AB, l'istesso punto G resterà centro dell'equilibrio, come da principio è stato. In oltre, essendo che la parte del solido CS è connessa alla libra mediante li due legami CA, IH, non è dubbio alcuno che se, tagliando detti due legami, ne aggiungeremo un solo MK, da essi due egualmente distante, trovandosi sotto di esso il centro della gravità del solido CS, non si muterà o moverà di sito, ma salverà l'istessa abitudine alla linea AH; e fatto l'istesso dall'altra parte IF, ciò è rotti i legami HI, BD ed aggiunto in mezzo il solo appendicolo NL, è parimente manifesto non esser lui per variare sito o disposizione rispetto alla libra AB: sì che, stando le parti di tutto il solido CF col medesimo rispetto alla libra AB che sempre son state, pendendo l'una, CS, dal punto M, e l'altra, SD, dal punto N, non è dubbio l'equilibrio farsi ancora dal punto medesimo G. E già comincierà ad apparire, come, pendendo dagli estremi termini della linea MN li due gravi, CS, maggiore, ed SD, minore, doventano di eguali momenti, e generano l'equilibrio nel punto G, facendo GN distanza maggiore della GM: e solo rimane, per esseguire compitamente il nostro intento, che dimostriamo, qual proporzione si trova fra il peso CS ed il peso SD, tale ritrovarsi tra la distanza NG e GM; il che non sarà difficile dimostrare. Per ciò che, essendo la linea MH metà dell'HA, e la NH metà della HB, sarà tutta la MN metà della total linea AB; della quale è metà ancora BG; onde esse due MN, GB saranno tra sé eguali: dalle quali trattone la comune parte GN, sarà la rimanente MG eguale alla rimanente NB; a cui è parimente eguale la NH; onde esse MG, NH, saranno ancora eguali; e posta communemente la parte GH, sarà la MH eguale alla GN. Ed avendo già dimostrato, MG agguagliare HN, qual proporzione avrà la linea MH alla HN, tale averà la NG distanza alla distanza GM: ma la proporzione MH ad HN è quella che ha KI a IL, e la doppia CI alla doppia ID, ed in somma il solido CS al solido SD (dei quali solidi le linee CI, ID sono altezze): adunque si conclude, la proporzione della distanza NG alla distanza GM esser l'istessa che ha la grandezza del solido CS alla grandezza del solido SD; la quale, come è manifesto, è quell'istessa che hanno le gravità dei medesimi solidi.
E da quanto si è detto parmi che apertamente si comprenda, come gli due gravi diseguali CS, SD non pure pesino egualmente pendendo da distanze le quali contrariamente abbino la medesima proporzione, ma di più come, in rei natura, sia il medesimo effetto, che se in distanze eguali si sospendessero pesi eguali: essendo che la gravità del peso CS in un certo modo virtualmente si diffonde oltre il sostegno G, e l'altra del peso SD dal medesimo si ritira, come, essaminando bene quanto si è detto circa la presente figura, ogni speculativo giudizio può comprendere. E, stante la medesima gravità dei pesi ed i medesimi termini delle suspensioni, quando bene si variassero le loro figure, riducendole in forme sferiche, conforme alle due X, Z, o in altre, non si dubiterà che il medesimo equilibrio sia per seguire; essendo la figura accidente di qualità ed impotente ad alterare la gravezza, che più presto dalla quantità deriva. Onde universalmente concluderemo, esser verissimo che pesi diseguali pesino egualmente, sospesi contrariamente da distanze diseguali, che abbino l'istessa proporzione dei pesi.
|