|
||||||
|
||||||
DOCUMENTS
elab.immagini
galileo
realtà virtuale
vrml
biomeccanica
esapodi
formula1
intelligenza
Papers
meccanica
sistemi
robotica
![]()
CARATTERISTICHE GENERALI
Le Reti Neurali
nascono dall’idea di poter riprodurre alcune delle funzioni e capacità del
cervello umano.
L’area di applicazione dominante delle Reti Neurali (RN) è il riconoscimento di pattern,
pattern recognition, e l’obiettivo fondamentale di tale
caratteristica è la classificazione: dato un input la rete è in
grado di analizzarlo e di formulare un output che corrisponda ad una
determinata e significativa categorizzazione.
Un esempio delle sue
potenzialità è la possibilità di riconoscere volti, voci etc.
La
classificazione della RN consiste nel
decidere a quale delle categorie indicategli, un pattern di input si
avvicina maggiormente in termini di distanza. In base al metodo di
misurazione di tale distanza, i classificatori di pattern si dividono in
due grandi categorie, numerici e non-numerici.
Le
tecniche numeriche misurano le distanze in modo deterministico e
statistico; tali misure possono essere considerate come misure effettuate
in uno spazio geometrico dei patterns.
Le tecniche non-numeriche sono
invece quelle legate a processi simbolici come i fuzzy
sets.
STRUTTURA
La RN è strutturata in
modo da essere un semplice modello della struttura e delle funzionalità
del cervello umano.
Una RN è
costituita da un determinato numero di neuroni e da connessioni tra essi
che rappresentano le connessioni sinottiche tra i neuroni biologici. La
funzione di un neurone biologico è quella di sommare i suoi input e
produrre un output qualora tale somma sia maggiore di un dato valore di
soglia.
Tali output vengono poi trasmessi a successivi neuroni
attraverso le giunzioni sinottiche; alcune di esse sono buone giunzioni
per cui il segnale trasmesso è alto, mentre altre sono cattive giunzioni
per cui il segnale trasmesso risulta più basso.
L’efficienza delle
giunzioni viene modellata considerando una fattore moltiplicativo (peso)
per ciascun input del neurone: una buona sinapsi avrà un peso maggiore di
quello della sinapsi cattiva. In linea di principio, in una RN, ogni unità può
essere connessa con qualunque altra unità.
Nella RN, quindi, un
neurone calcola la somma pesata I, degli input xi, (vedi Eq.1) e la
confronta con un valore di soglia, se la somma risulta maggiore di tale
soglia il neurone "si accende" e trasmette un output.
![]() (1)
(1)
dove wi rappresenta il peso dell’ i-esimo
neurone.
Un modo alternativo e
maggiormente usato per raggiungere il medesimo effetto è quello di
considerare la soglia come un ulteriore valore di input fissato sempre
pari a 1:
![]() (2)
(2)
L’output di un neurone è dato dalla trasformazione dell’input I,
cioè della somma pesata, tramite una funzione detta di
attivazione. Analogamente quindi, ai neuroni biologi, la funzione di
attivazione ha due principali caratteristiche: deve tenere conto della
soglia e non deve mai superare un livello di saturazione.
La funzione
può essere, ad esempio, a gradino:
![]() (3)
(3)
o una funzione continua differenziabile detta logistica o sigmoide, Eq. 4, nel caso in cui la soglia sia considerata come un ulteriore input pari a 1.
![]() (4)
(4)
E’
importante sottolineare che il modo con cui una RN risponde ad un pattern dipende
interamente dai pesi delle connessioni.
APPRENDIMENTO
Il principio guida
che permette alla rete di apprendere è quello di lasciare che la rete
impari dai suoi errori.
Le reti hanno, inizialmente, dei pesi scelti a
caso (in particolare valori normalizzati, ovvero compresi fra 0 e 1 o tra
-0.5 e +0.5); a questo punto esistono diversi metodi con cui le reti
modificano automaticamente questi pesi fino ad assegnare loro quei valori
che consentono di rispondere nel modo desiderato ad una certa stimolazione
esterna.
Tutti i metodi di apprendimento si dividono in due classi:
metodo supervisionato e non-supervisionato. Quello
maggiormente considerato è quello supervisionato in cui esiste una specie
di "insegnante" esterno che di volta in volta dice alla rete quale è la
prestazione desiderata.
La rete si modifica in conseguenza a tale
insegnamento cosicché, dopo un certo numero di volte (dell’ordine delle
migliaia) che le è stato detto quale è l’output appropriato per un certo
input, diventa capace di produrre da sola l’output corretto per ogni
input.
Un esempio di apprendimento supervisionato è quello della
back-propagation (BP), cioè della propagazione all’indietro
dell’errore: la rete calcola, per ogni unità di output, l’errore cioè la
differenza tra lo stato di attivazione prodotto dalla rete e quello
stabilito nell’input di insegnamento; questo errore serve a modificare i
pesi delle connessioni tra i neuroni.
Nei casi di apprendimento
non-supervisionato la rete impara scoprendo regolarità negli stimoli senza
che nessuno le dica dall’esterno quali sono queste regolarità. Così accade
nelle reti che sviluppano "mappe di tratti" (feature maps) di
Kohonen.
Le reti non danno risultati completamente corretti o
completamente sbagliati, ma solo approssimativamente corretti o sbagliati
(non 1 o 0 ma 0.96 o 0.03). Inoltre, se una rete ha imparato, ad esempio,
a dare B in risposta ad A, quando le si presenta uno stimolo A’ che sia
simile ad A, risponde automaticamente e spontaneamente in modo sensato: o
dà la stessa risposta data per A, cioè B, o risponde con B’, cioè dà una
risposta simile a quella data per A.
Questa capacità di estrapolare, di
rispondere sensatamente al nuovo, è una delle più importanti proprietà
delle RN, e uno dei loro principali
vantaggi rispetto ai sistemi simbolici tradizionali.
Le principali
RN utilizzate oggi, differenziate per
struttura e quindi per funzionalità e scopo, sono: Multilayer Perceptron
con Back Propagation come metodo di apprendimento, Reti di Hopfield e Reti
di Kohonen.
THE MULTILAYER PERCEPTRON E
BACK PROPAGATION
Il Perceptron è stato la prima RN utilizzata ed era costituita da un singolo
strato di neuroni che riceveva un input e calcolava direttamente
l’output.
In questo modo la rete era limitata nel calcolo di una
singola retta, nello spazio geometrico dei pattern, di separazione tra le
classi senza essere quindi in grado di classificare problemi
complessi.
Per poter superare il limite di separabilità lineare delle
classi mantenendo intatta la capacità di apprendere, sono state eseguite
alcune variazioni strutturali aggiungendo uno o più strati di neuroni in
modo che ogni neurone di ciascuno strato riceva come input l’output dei
neuroni dello strato precedente e che l’output di rete sia quello
calcolato dall’ultimo strato.
La rete così ottenuta viene chiamata
Multilayer Perceptron.
I
neuroni (o unità) che costituiscono questo tipo di reti, quindi, sono
organizzati in strati, layer: uno strato di input, uno di output e
un certo numero di strati intermedi tra input e output detti nascosti,
hidden.
In tali reti la funzione di attivazione non è a gradino
ma è la funzione sigmoide. Le unità dello strato di input hanno il solo
compito di trasmettere i valori di input allo strato successivo calcolando
solo la somma pesata degli input.
Il fatto di utilizzare la
funzione sigmoide per calcolare l’output di una rete piuttosto che una
funzione a gradino permette di suddividere la spazio dei pattern con linee
curve piuttosto che semplici rette in modo da classificare oggetti
complessi.
Per visualizzare come funziona tale rete chiamiamo
Tpj l’output corretto, o target, per il pattern
p e il neurone di output j, Opj l’output calcolato dal
j-esimo neurone per il medesimo pattern p e wij il
peso legato alla connessione tra il neurone i e il neurone
j
L’algoritmo di apprendimento della rete è il
seguente:
1) Inizialmente si pongono i valori dei pesi
casuali compresi fra [0,1] o [-0.5,0.5] in modo che siano piccoli e
normalizzati.
2) Si presenta un pattern p di input alla
rete: xp = (x0, x1, x2, ..., xn-1) con x0=1 e un vettore costituito dai valori di output corretti
Tp = (T0,T 1,
T2, ..., Tm-1). In questo modo la
rete sarà costituita da (n-1) neuroni di input e (m-1) neuroni di
output.
3) Per ogni layer si calcola la somma pesata degli
input e il suo valore di attivazione, ovvero l’output dato dall’equazione
(4) con I dato dalla (2).
Dopo aver eseguito l’ultimo punto per
tutti gli strati, si devono modificare i pesi in modo che l’output della
rete, cioè l’output dell’ultimo strato di neuroni, si avvicini sempre più
a quello desiderato. Per questo viene definita una funzione errore Ep proporzionale al quadrato della differenza tra output e
target per tutti i neuroni di output:
![]() (5)
(5)
A
questo punto si applica la Back Propagation ovvero di variano i
pesi in modo che l’errore Ep tenda a zero partendo
dall’ultimo strato verso il primo (ecco il perché della propagazione
all’indietro).
Si definisce, per il pattern corrente p, una variazione
D wij del peso wij tra il neurone
i e quello j data da:
![]() (6)
(6)
dove a è il coefficiente di apprendimento (learning rate), ![]() è il momento e
è il momento e ![]() p-1wij è la variazione del medesimo peso calcolata al pattern
precedente.
p-1wij è la variazione del medesimo peso calcolata al pattern
precedente.
I nuovi pesi saranno quindi dati da:
![]() (7)
(7)
La variazione dei pesi viene calcolata a partire dallo strato di neuroni di output e a ritroso verso il primo strato nascosto. Le derivate possono essere calcolate:
![]() (8)
(8)
dove Ai è il valore del’i-esimo neurone dello
strato che si sta considerando mentre ![]() j è:
j è:
![]() (9)
(9)
se si sta considerando lo strato di output, mentre per tutti gli altri strati intermedi è:
![]() (10)
(10)
dove le somme sono estese a tutti i neuroni dello strato successivo (considerando l’ordine da input ad output) a quello che si sta considerando.
Per far apprendere una rete è infatti necessario mostrarle un certo
numero di volte, circa 1000, un determinato numero di diversi pattern per
ognuno dei quali verranno modificati i pesi in modo da diminuire l’errore
e avvicinare i valori di output al target.
Tale procedimento viene
eseguito un certo numero di volte fino a quando l’errore risulta minore ad
un certo valore prefissato o non diminuisce ulteriormente. A questo punto
la rete ha appreso, i pesi sono fissati ed è pronta per classificare un
nuovo input di cui non si conosce il target.
I parametri ![]() e
e ![]() vengono scelti dall’utente con
valori compresi fra 0 e 1 (o meglio tra 0.2 e 0.8 in modo che non siano
troppo vicini agli estremi dell’intervallo): i valori fissati sono
caratteristici della rete. In particolare a è legata alla convergenza
della rete, maggiore è il suo valore e maggiore è la velocità di
convergenza della rete; aumentando però tale convergenza è possibile che
la rete converga ad un minimo dell’errore non assoluto ma locale
(minimi locali) a cui non corrisponde un output corretto.
vengono scelti dall’utente con
valori compresi fra 0 e 1 (o meglio tra 0.2 e 0.8 in modo che non siano
troppo vicini agli estremi dell’intervallo): i valori fissati sono
caratteristici della rete. In particolare a è legata alla convergenza
della rete, maggiore è il suo valore e maggiore è la velocità di
convergenza della rete; aumentando però tale convergenza è possibile che
la rete converga ad un minimo dell’errore non assoluto ma locale
(minimi locali) a cui non corrisponde un output corretto.
Per
evitare questo comportamento si può abbassare il valore di ![]() per rallentare la convergenza oppure,
quando si considerano casi non reali, si può aggiungere rumore ai pattern
di input o, come nel nostro caso, si aggiunge il termine momento
per rallentare la convergenza oppure,
quando si considerano casi non reali, si può aggiungere rumore ai pattern
di input o, come nel nostro caso, si aggiunge il termine momento ![]() in modo da non dover
rallentare la convergenza.
in modo da non dover
rallentare la convergenza.
Il termine legato a ![]() permette di produrre grandi
variazioni dei pesi per poter "saltare" i minimi locali e piccole
variazioni quando i cambiamenti sono piccoli (cioè quando
permette di produrre grandi
variazioni dei pesi per poter "saltare" i minimi locali e piccole
variazioni quando i cambiamenti sono piccoli (cioè quando ![]() p-1 è
piccolo).
p-1 è
piccolo).
Problemi diversi, più o meno complessi, vengono risolti
da diverse reti neurali caratterizzate da un diverso numero di neuroni nel
hidden layer e da determinati valori di ![]() e
e ![]() .
.
In linea generale man mano che
il problema si complica dovrebbe essere necessario aumentare il numero di
strati intermedi, ma per il teorema di Kolmogorov è sufficiente aumentare
solo il numero dei neuroni mantenendo un unico strato
intermedio.
Infine, poiché l’apprendimento di queste reti consiste
nella modificazione dei pesi, è evidente che tutto il decorso
dell’apprendimento e il suo risultato finale varieranno da rete a
rete.
Quindi se si ripete lo stesso esperimento su reti diverse, cioè
aventi assegnazione iniziale di pesi differenti (diverse scelta casuale
dei pesi), non si possono aspettare risultati identici ma soltanto
risultati simili.
Il metodo BP di apprendimento viene anche
chiamato gradiente discendente in quanto le variazioni vengono
eseguite verso il minimo della funzione
errore.
Generalizzazione della RN
Una delle maggiori
caratteristiche delle RN è la loro
abilità a generalizzare ovvero a classificare con successo pattern che non
sono stati precedentemente mostrati (cioè mostrati durante
l’apprendimento).
Un vantaggio della rete a multi strati è quello
di poter classificare input rumorosi: ad essi verranno associate le classi
relative all’input senza rumore. Questa abilità permette di applicare con
successo queste reti a problemi reali, e quindi rumorosi, con risultati
migliori rispetto a quelli ottenuti con altri metodi di riconoscimento di
pattern o sistemi esperti.
Nel caso in cui l’input sia diverso da
quelli già classificati dalla rete nel ciclo di apprendimento, l’output
sarà meno preciso ed in particolare si posso considerare due casi. Se il
pattern di input è posto tra due pattern già visti; la rete lo classifica
come il pattern in esso dominante.
Se invece non è simile a nessun
pattern già visto, la classificazione avviene con un errore maggiore (se
si ottiene un errore del 10% con i pattern già visti dalla rete, si può
ottenere un errore di circa il 13-20% con pattern non ancora
classificati).
RETI DI
HOPFIELD
La funzione principale delle Reti di Hopfield è
quella di riconoscere pattern molto rumorosi come pattern che sono stati
"immagazzinati nella sua memoria" cioè già classificati: ad un pattern
rumoroso viene associato in output un pattern perfetto.
La Rete di
Hopfield è costituita da neuroni non suddivisi in strati, ognuno di essi
connesso a tutti gli altri (rete fully-connected).
I pesi delle
connessioni tra i neuroni sono simmetrici:
il peso della
connessione tra neurone i e neurone j, wij, è uguale
al peso della connessione nell’altra direzione tra il neurone j e il
neurone i, wij = wji.
Ciascun
neurone ha una soglia interna e la funzione di attivazione per calcolare
l’output dalla somma pesata dell’input è a gradino (Eq. (3)).
La rete
può avere solo due stati di input: binario (0,1) o bipolare
(-1,+1).
Gli input vengono mostrati a tutti i neuroni della rete
contemporaneamente; a questo punto la rete viene lasciata da sola per il
ciclo di apprendimento fino alla convergenza ottenuta quando i valori dei
neuroni non cambiano più. Tali valori ultimi rappresentano l’output della
rete. Poiché tutti i neuroni sono connessi a tutti, il valore di un
neurone influenza il valore di tutti gli altri; man mano che la rete passa
attraverso stadi intermedi cerca di raggiungere un compromesso tra tutti i
valori dei neuroni, e lo stadio finale è dato dal miglior
compromesso che la rete possa trovare.
Nel ciclo di apprendimento
ogni output di un neurone è un nuovo input per lo stesso neurone che
produrrà un nuovo output e così via.
Supponiamo di dover
immagazzinare nella rete un cerco numero M di pattern, indichiamo con
xi![]() l’input all’i-esimo neurone
corrispondente all’s-esimo pattern e con wij il peso
dal i-esimo al j-esimo neurone.
l’input all’i-esimo neurone
corrispondente all’s-esimo pattern e con wij il peso
dal i-esimo al j-esimo neurone.
L’algoritmo di apprendimento è il
seguente:
1) Inizialmente si assegnano i pesi delle connessioni
tra i neuroni:
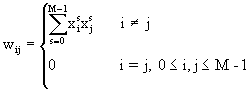 (11)
(11)
dove i valori di x possono essere solo +1 e -1 oppure solo 0 e 1.
2) Assegnare ai neuroni i valori di input di un pattern
sconosciuto e calcolare i relativi output utilizzando una funzione a
gradino dopo aver assegnato una soglia per ciascun neurone.
Indichiamo
con Ti il valore di soglia per l’i-esimo
neurone:
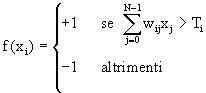 (12)
(12)
dove N è il numero di neuroni. L’equazione (9) vale nel caso in cui
si stia considerando solo valori +1 e -1 altrimenti l’output di ciascun
neurone potrà assumere valori rispettivamente pari a 1 e
0.
3) Si ripete l’equazione (9), aggiornando i valori di
input xi con i nuovi valori f(xi)
di output, fino a quando questi ultimi non variano più.
E’
possibile definire un energia E della rete di Hopfield nel modo
seguente:
![]() (13)
(13)
dove le somme sono estese a tutti i neuroni che costituiscono la
rete e xi sono gli output del i-esimo neurone e che
costituiranno i successivi input dei medesimi neuroni. I pesi della rete
contengono le informazioni di tutti i pattern (vedi Eq. 8) e quindi tutti
i pattern sono inclusi nell’energia così definita.
Qualora un
neurone subisca un incremento di attivazione dxi l’energia varierà della
quantità:
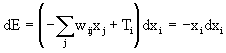 (14)
(14)
che è nulla o negativa. Infatti, qualora xi passi dal valore -1 al
valore +1 (o dal valore 0 al valore 1), sarà xi > 0
e dxi > 0, ed analogamente per gli altri casi
possibili. Dunque l’energia E non può che decrescere. Aggiornando gli
output sequenzialmente secondo la relazione (9) la rete, dopo un certo
numero di iterazioni, si stabilizza nello stato di minima
energia.
Quindi l’energia, che rappresenta tutti i pattern
considerati, è una funzione con minimi in corrispondenza dei pattern
immagazzinati nella rete.
Un pattern sconosciuto rappresenta un
particolare punto sull’iper-superficie dell’energia, e, man mano che la
rete calcola i valori di output verso lo stato finale, il punto si muove
sulla iper-superficie verso un punto di minimo: questa zona di attrazione
rappresenta lo stato stabile della rete, ovvero la rete è stata in grado
di associare ad un pattern sconosciuto (un punto nello spazio
dell’energia) una pattern già visto dalla rete (cioè un punto di minimo
dell’energia).
Eventuali errori nella ricostruzione di un pattern,
cioè quando vengono associati a pattern sconosciuti pattern in output
sbagliati, possono comparire quando sono stati immagazzinati nella rete
più di 0.5N con N numero di neuroni della rete. Questi pattern sbagliati
sono comunque stati stabili di output della rete a cui però non
corrisponde nessun pattern immagazzinato; c’è stata interferenza e
sovrapposizione tra i pattern immagazzinati da formare uno stato con
energia minima locale (come per le reti con back propagation) che la rete
considera come soluzione accettabile. Questi stati vengono chiamati
stati metastabili.
RETI DI
KOHONEN
Le Reti di Kohonen permettono di classificare
oggetti senza la supervisione esterna. Nascono dallo studio della
topologia della corteccia del cervello umano. Queste reti tengono conto
non solo delle connessioni sinottiche tra neuroni ma anche della influenza
che può avere un neurone sul vicino. E’ stato osservato che, nel caso
biologico, i neuroni che sono fisicamente vicini a neuroni attivi hanno i
legami più forti mentre quelli ad una particolare distanza hanno legami
inibitori. A questa caratteristica Kohonen attribuisce uno sviluppo nella
capacità di realizzare delle mappe topologiche localizzate nel cervello.
Questa caratteristica è stata modellata da Kohonen restringendo la
variazione dei pesi ai neuroni vicini ad un neurone scelto.
Una
Rete di Kohonen è costituita da una
serie di neuroni di input che, come per le reti a multi strati, servono
solo a calcolare la somma pesata di tutti gli input e da un singolo strato
bidimensionale di neuroni, sono cioè organizzati su una griglia posta su
un piano; tali neuroni calcolano l’output della rete. Ciascun neurone di
input è connesso a tutti i neuroni della griglia.
L’apprendimento è
legato alle interconnessioni laterali tra neuroni vicini. L’algoritmo di
apprendimento di questo tipo di RN è il
seguente:
1) Si definiscono con wij(t)
(0 ![]() i
i ![]() n-1 dove n è il numero di input) il
peso tra il neurone i-esimo di input e il neurone j-esimo della griglia al
tempo t. Con "tempo" si indica il passaggio del pattern di apprendimento).
I valori dei pesi vengono inizialmente posti casualmente tra 0 e 1. Si
pone come valore di Nj(0) il maggiore possibile
(Nj() dovrebbe essere il numero di neuroni vicini al
j-esimo neurone).
n-1 dove n è il numero di input) il
peso tra il neurone i-esimo di input e il neurone j-esimo della griglia al
tempo t. Con "tempo" si indica il passaggio del pattern di apprendimento).
I valori dei pesi vengono inizialmente posti casualmente tra 0 e 1. Si
pone come valore di Nj(0) il maggiore possibile
(Nj() dovrebbe essere il numero di neuroni vicini al
j-esimo neurone).
2) Si presenta un input: x0(t), x1(t), x2(t),...,xn-1(t)
dove xi(t) è l’i-esimo
input.
3) Si calcolano le distanze dj
tra l’input e ciascun neurone di output j:
![]() (15)
(15)
4) Si seleziona il neurone a cui corrisponde la distanza
minima. Indichiamo con j* tale neurone.
5) Si modificano i
pesi dal neurone di input e il neurone j* e tutti i suoi vicini definiti
all’interno della superficie definita da Nj*(t).
I
nuovi pesi sono:
![]() (16)
(16)
Il
termine ![]() (t) è la
funzione guadagno (o velocità di adattazione) (0
(t) è la
funzione guadagno (o velocità di adattazione) (0 ![]()
![]() (t)
(t) ![]() 1) che decresce nel tempo in modo
da rallentare di volta in volta l’adattamento dei pesi.
1) che decresce nel tempo in modo
da rallentare di volta in volta l’adattamento dei pesi.
Anche le
dimensioni di Nj*(t) decrescono nel tempo in modo da
individuare una regione di neuroni sulla griglia.
6) Si ripete tutto a partire dal punto 2).
Si osserva
come l’algoritmo di apprendimento di questa rete è molto più semplice di
quello delle reti precedenti in cui è stato necessario calcolare una
derivata; nel caso di Kohonen si confronta semplicemente un pattern di
input e il vettore dei pesi (vedi Eq.15). Il neurone con il vettore dei
pesi più vicino al pattern di input viene selezionato (j*); questo nodo
"claims" the input vector e modifica il suo vettore dei pesi in modo da
allinearlo a quello degli input x cioè in modo da diminuire dj.
Si può inoltre osservare che vengono modificati anche
i vettori dei pesi dei neuroni vicini a j*; il motivo di ciò è che la rete
sta cercando di creare regioni costituite da un ampio set di valori
attorno all’input con cui apprende (cioè non fa corrispondere un solo
valore per un input ma un set di valori), di conseguenza, i vettori che
sono spazialmente vicini ai valori di training saranno comunque
classificati correttamente anche se la rete non li ha mai visti.
Questo
dimostra le proprietà di generalizzare della rete.
Consideriamo ora
come la rete apprende cioè come vengono variati i pesi. La funzione
guadagno è una funzione decrescente che inizialmente viene mantenuta alta
(> 0.5) in modo da modificare velocemente i pesi verso una prima
mappatura approssimativa.
In seguito vengono eseguite delle mappature
fini avvicinando i vettori dei pesi a quelli di input, per eseguire queste
variazioni fini si riduce ![]() sempre più.
sempre più.
Kohonen suggerisce un guadagno che decresce
linearmente con il numero dei passaggi. Il processo di apprendimento dal
punto 2) al 6), deve essere eseguito dalle 100 alle 1000 volte circa. In
questa rete le somiglianze tra le classi vengono misurate con la distanza
euclidea.
La regione dei vicini può essere scelta essere un
quadrato, un cerchio o un esagono. Il valore di Nj*
(cioè il numero di vicini al neurone prescelto) deve essere scelto il
maggiore possibile all’inizio e decrescere anch’esso lentamente
all’aumentare dei cicli di apprendimento.
APPROFONDIMENTI TEORICI
Definiamo l'errore
della rete in funzione del quadrato della differenza tra l'output attuale
e quello desiderato per tutti i pattern che devono essere
appresi.
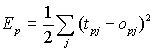 (1)
(1)
Il coefficiente "1/2" non altera la sostanza della formula ma presenta il vantaggio di semplificare alcuni calcoli successivi (*). Il valore di attivazione di ciascun nodo j al pattern p consiste nella somma pesata con w dei precedenti output o.
![]() (2)
(2)
A sua volta ciascun output è dato dalla funzione di soglia f, nella fattispecie una sigmoide, applicata alla somma pesata.
![]() (3)
(3)
Considerando il rapporto tra E e w possiamo scrivere
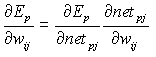 (4)
(4)
e soffermandoci sul secondo fattore evidenziamo che
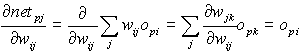 (5)
(5)
Indicando
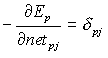 (6)
(6)
diventa.
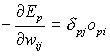 (7)
(7)
Inoltre si può scrivere
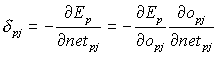 (8)
(8)
ed essendo il secondo fattore Df(x)/Dx esso equivale a.
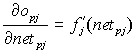 (9)
(9)
Considerando poi il primo fattore, e calcolando la derivata di E rispetto ad o, otteniamo.
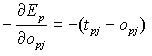 (10)
(10)
Perciò, rimoltiplicando i fattori otteniamo.
![]() (11)
(11)
Questo risultato presuppone che siano direttamente valutabili il target t e l'output o, e la sua validità è limitata al solo livello di output. Per i livelli intermedi consideriamo nuovamente il primo dei fattori in cui era stato scomposto g e notiamo che;
 (12)
(12)
rimoltiplicando ancora i fattori abbiamo infine.
![]() (13)
(13)
Questa equazione rappresenta la variazione dell'errore in relazione ai pesi della rete, e fornisce un criterio per ridurre tale errore. A questo punto non resta che calcolare la derivata di f(net).
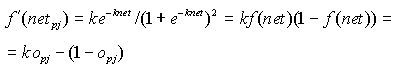 (14)
(14)
ESEMPIO
Scaricate questo programma che genera una rete neurale:
Neural Networks Kit di Southern
Scientific